ЛАТВИЯ. ОБРАЗОВАНИЕ
20.04.2023


Армен Халатян
Хозяин своего дела
НЕХВАТКА ИНЖЕНЕРОВ

-
Участники дискуссии:
1672 -
Последняя реплика:
больше месяца назад
Анатолий Бодров,
Леонид Соколов,
Марк Козыренко,
arvid miezis,
Леонид Радченко,
Анатолий Первый,
Владимир Иванов,
Юрий Васильевич Мартинович,
Марина Зимина,
Игорь Александрович Бессмертный,
Kęstutis Čeponis,
Иван Киплинг,
Roman Romanovs,
Victoria Dorais,
Андрей Батурин
Ведущая латвийская ежедневная газета Diena опубликовала статью о ситуации в школьном образовании под заголовком "Нехватка инженеров начинается в школе".
Статья настолько насыщенная примерами и выводами, что привожу её практически целиком.
Статья начинается с предположения, что причина падения интереса к физике, химии и биологии связана с плохим преподаванием математики в начальной школе. К сожалению результаты диагностических работ за 30 лет сравнивать невозможно, так как они все время упрощались: исчезли устные вопросы по Геометрии, убрали целый ряд текстовых задач.
В диагностической работе 6 классе задачу связанную с пониманием масштаба и пропорций (найти реальную длину экватора, зная её на глобусе) смогли решить около 28% учашихся, насколько далеко надо расположить Луну от Земли на модели, зная реальное расстояние – 16%
Хотя задачи похожи разница в результатах объясняется тем, что в первом случае более высока вероятность угадать Авторы указывают, что «вместо того, чтобы учить пониманию, расчет в этих упражнениях методично отделяется от основного смысла — пропорций.
Вместо одной универсальной методики, которая давала бы понимание всех видов интересных задач, учителя без устали учат запоминанию трех формул, каждая из которых соответствует одному из трех возможных неизвестных. Неизвестный процент количества — одна формула, неизвестная часть количества, но известный процент, вторая формула, неизвестное количество, третья формула. Формулы известны детям, но процент разрешимости ниже, чем у метода угадывания.
А именно, если бы учащиеся угадали, то не менее 33% дали бы правильное решение.» «В экзаменационной работе за 9 класс видно, что треть учащихся не имеют представления о математических понятиях — что такое квадрат, что такое ромб, какие стороны треугольника определяют синус, какой косинус и т. д.
Другими словами, принижение геометрии путем невыделения ее как отдельной дисциплины имеет последствия. Если учащийся не понимает понятие площади, трудно ожидать понимания понятия квадрата в алгебре. Можно предположить, что более трети учащихся застряли в понимании понятий плоскости и пространства или не имеют возможности умножать и делить натуральные числа.» Учителя видят причины в том, что «ученику не показывают принципы математики. Вместо этого учат, как вычислять примеры, но ученик не знает, что делать, если пример хоть немного изменить. Корень многих бед заложен уже в начальной школе , где не даются фундаментальные основы. В 7 классе мы видим, что текстовая грамотность очень слабая.
Ученики не умеют читать информацию даже из простой инфографики, которая специально разработана, чтобы ее было легче понять" Дальше автор описывает как слабые знания математики влияют на понимание естественных наук: физики, химии, биологии.
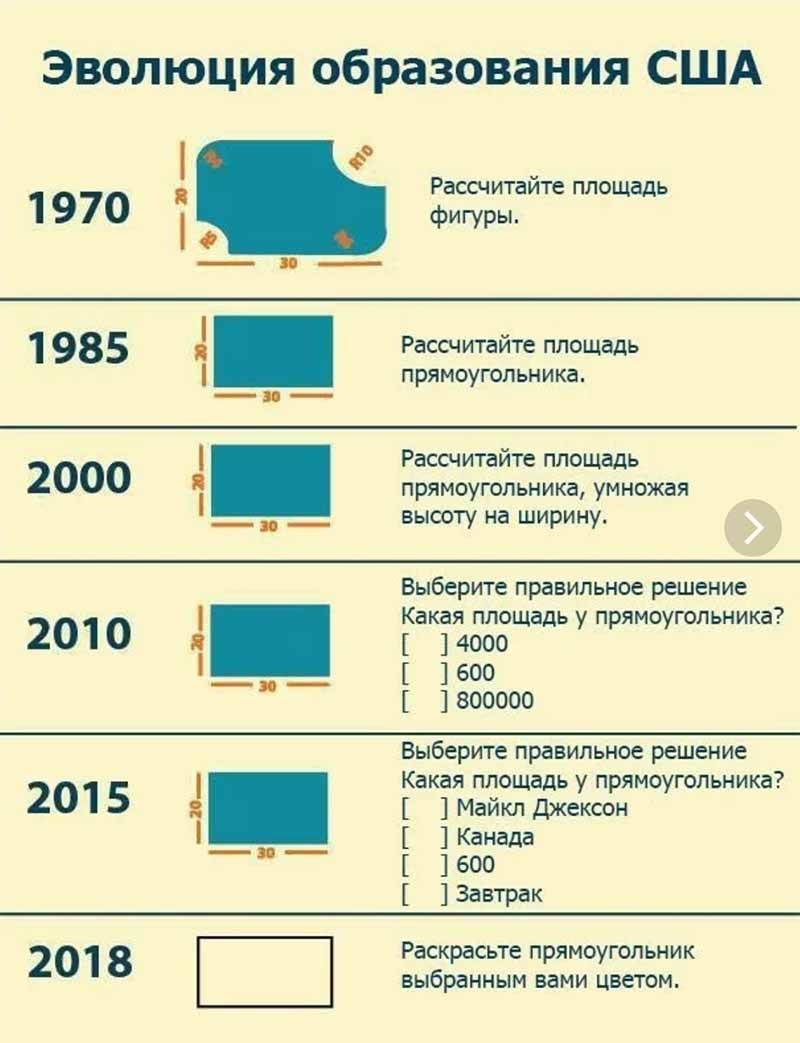
Во-первых, умножение, действия с дробями, деление на простые множители, нахождение наибольшего общего делителя и т. д. составляют основу любой научной задачи. В неорганической химии для записи реакции воды, например, с серной кислотой потребуется умение работать с натуральными числами и выполнять указанные операции.
Если этого навыка нет, та часть урока химии, где учитель демонстрирует эксперимент или рассказывает об общих вещах, может быть интересна ученику, но решение задач вызовет у него отвращение и протест, потому что он вообще не может их решить! Также в физике необходимы навыки операций с натуральными числами, понимание операций с показателями степени, без которых невозможен перевод единиц измерения и т.д. Большая часть этих знаний приобретается в первых шести классах.
Пропорции и проценты особенно важны, ведь без этого элемента не могут обойтись научные тесты. Пропорции и проценты в различных задачах биологии, физики и химии встречаются примерно в пятой части случаев, и именно эти задачи не решаются больше всего. Я делаю этот вывод с того времени, когда сам преподавал физику в начальной школе. Учитывая, что с тех пор прошло 20 лет, возможно, доля процентов и пропорций в тестах по естественным наукам уже сократилась, однако в природе, в практической жизни ни одна научная задача не может быть решена без математических навыков.
Иными словами, утверждение о том, что средняя школа не в состоянии подготовить полноценных студентов инженерных и точных наук, верно, но вина в первую очередь не в средней школе.
База находится в начальной школе и, возможно, даже в дошкольном возрасте.
Статья настолько насыщенная примерами и выводами, что привожу её практически целиком.
Статья начинается с предположения, что причина падения интереса к физике, химии и биологии связана с плохим преподаванием математики в начальной школе. К сожалению результаты диагностических работ за 30 лет сравнивать невозможно, так как они все время упрощались: исчезли устные вопросы по Геометрии, убрали целый ряд текстовых задач.
В диагностической работе 6 классе задачу связанную с пониманием масштаба и пропорций (найти реальную длину экватора, зная её на глобусе) смогли решить около 28% учашихся, насколько далеко надо расположить Луну от Земли на модели, зная реальное расстояние – 16%
Хотя задачи похожи разница в результатах объясняется тем, что в первом случае более высока вероятность угадать Авторы указывают, что «вместо того, чтобы учить пониманию, расчет в этих упражнениях методично отделяется от основного смысла — пропорций.
Вместо одной универсальной методики, которая давала бы понимание всех видов интересных задач, учителя без устали учат запоминанию трех формул, каждая из которых соответствует одному из трех возможных неизвестных. Неизвестный процент количества — одна формула, неизвестная часть количества, но известный процент, вторая формула, неизвестное количество, третья формула. Формулы известны детям, но процент разрешимости ниже, чем у метода угадывания.
А именно, если бы учащиеся угадали, то не менее 33% дали бы правильное решение.» «В экзаменационной работе за 9 класс видно, что треть учащихся не имеют представления о математических понятиях — что такое квадрат, что такое ромб, какие стороны треугольника определяют синус, какой косинус и т. д.
Другими словами, принижение геометрии путем невыделения ее как отдельной дисциплины имеет последствия. Если учащийся не понимает понятие площади, трудно ожидать понимания понятия квадрата в алгебре. Можно предположить, что более трети учащихся застряли в понимании понятий плоскости и пространства или не имеют возможности умножать и делить натуральные числа.» Учителя видят причины в том, что «ученику не показывают принципы математики. Вместо этого учат, как вычислять примеры, но ученик не знает, что делать, если пример хоть немного изменить. Корень многих бед заложен уже в начальной школе , где не даются фундаментальные основы. В 7 классе мы видим, что текстовая грамотность очень слабая.
Ученики не умеют читать информацию даже из простой инфографики, которая специально разработана, чтобы ее было легче понять" Дальше автор описывает как слабые знания математики влияют на понимание естественных наук: физики, химии, биологии.

Во-первых, умножение, действия с дробями, деление на простые множители, нахождение наибольшего общего делителя и т. д. составляют основу любой научной задачи. В неорганической химии для записи реакции воды, например, с серной кислотой потребуется умение работать с натуральными числами и выполнять указанные операции.
Если этого навыка нет, та часть урока химии, где учитель демонстрирует эксперимент или рассказывает об общих вещах, может быть интересна ученику, но решение задач вызовет у него отвращение и протест, потому что он вообще не может их решить! Также в физике необходимы навыки операций с натуральными числами, понимание операций с показателями степени, без которых невозможен перевод единиц измерения и т.д. Большая часть этих знаний приобретается в первых шести классах.
Пропорции и проценты особенно важны, ведь без этого элемента не могут обойтись научные тесты. Пропорции и проценты в различных задачах биологии, физики и химии встречаются примерно в пятой части случаев, и именно эти задачи не решаются больше всего. Я делаю этот вывод с того времени, когда сам преподавал физику в начальной школе. Учитывая, что с тех пор прошло 20 лет, возможно, доля процентов и пропорций в тестах по естественным наукам уже сократилась, однако в природе, в практической жизни ни одна научная задача не может быть решена без математических навыков.
Иными словами, утверждение о том, что средняя школа не в состоянии подготовить полноценных студентов инженерных и точных наук, верно, но вина в первую очередь не в средней школе.
База находится в начальной школе и, возможно, даже в дошкольном возрасте.
Дискуссия
Еще по теме
Еще по теме


Дмитрий Змиёв
Консультант по бизнес-процессам
Система образования слаба
Нужны глобальные реформы


Юрий Иванович Кутырев
Неравнодушный человек, сохранивший память и совесть.
НОВОЕ СЛОВО В ЛАТВИИ
УРА! у нас все сделано. можем взяться за слова


Игорь Пименов
Физик, экономист, политик
ИЛИ ХОРОВОЙ КРУЖОК, ИЛИ РОДНОЙ ЯЗЫК


Вадим Фальков
Журналист, депутат Рижской думы
Рига пошла в школу
Что происходит в столичных учебных заведениях




